State Hash
The State Hash is used to ensure the integrity of the data in the Pactus blockchain. It serves as a unique identifier or fingerprint of the current state of the blockchain, allowing all nodes to verify that their data matches that of the other nodes. This helps to prevent any tampering or inconsistencies in the data, ensuring the accuracy and consistency of the blockchain.
Merkle Tree
In cryptography and computer science, a hash tree or Merkle tree is a tree in which every leaf node is labelled with the cryptographic hash of a data block, and every non-leaf node is labelled with the cryptographic hash of the labels of its child nodes. Hash trees allow efficient and secure verification of the contents of large data structures.
From Wikipedia
A Hash tree or Merkle tree is a data structure that used by many blockchains to solve this problem: “How can data be securely stored and verified in a decentralized network?”
By using a Merkle tree, nodes can easily verify that they store the same data without having to share the entire dataset. Additionally, this helps to prevent any tampering with the data, as any changes made to the data would cause inconsistencies in the Merkle tree and can be easily detected by the network.
State Merkle Trees
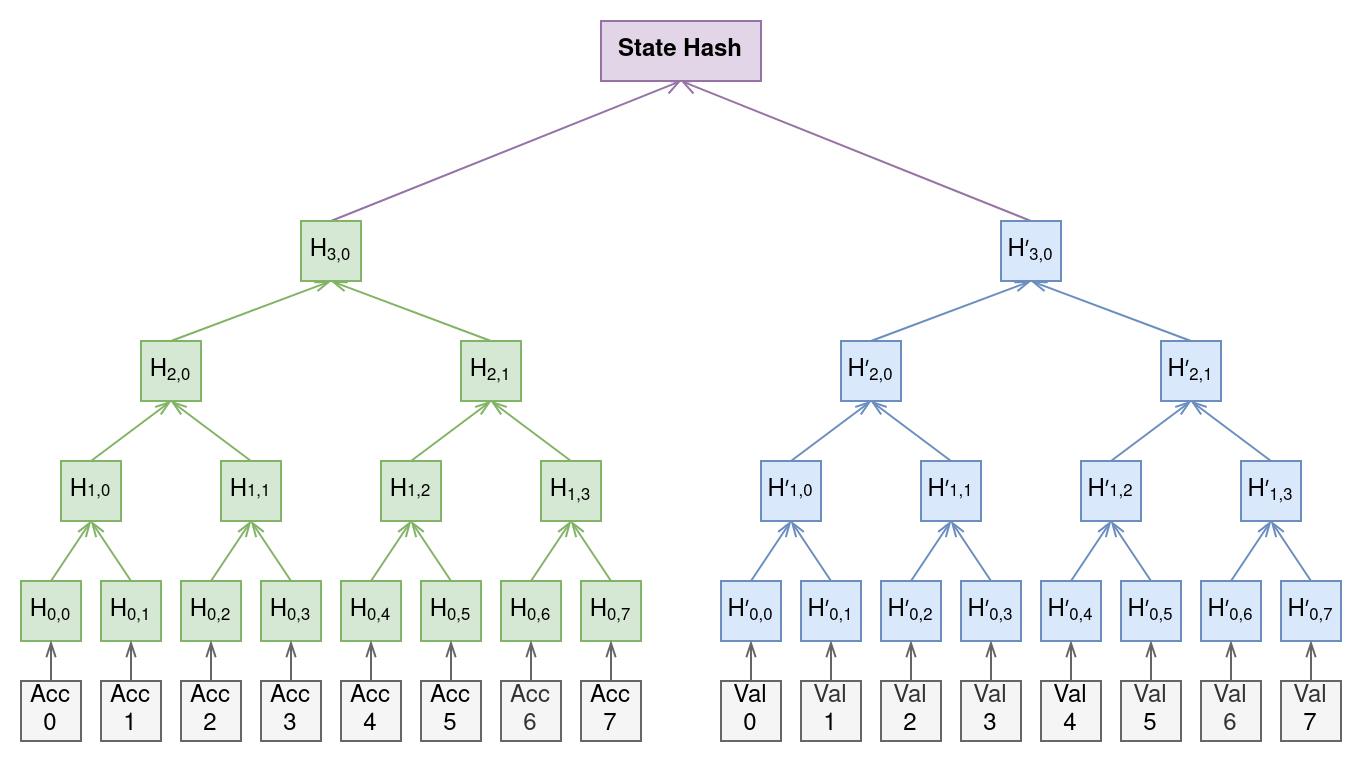
In Pactus, the Merkle tree is used to verify the state of the blockchain in each block. The state hash in each block is calculated by taking the hash of two Merkle trees: the accounts Merkle tree and the validators Merkle tree. Each leaf in these trees contains the hash of the associated account or validator. By using the state hash, all nodes in the network can ensure they have the same data stored.
Scalability of Merkle Tree
Using a Merkle tree to calculate the state of the blockchain can be challenging because when the number of accounts is large, calculating the root hash can be difficult. In other words, a simple Merkle tree may not be scalable because calculating all the leaf and node hashes requires a significant amount of computation.
In Pactus, all accounts and validators have unique and sequential numbers. This means that each account and validator has a dedicated account number that helps us to calculate the hash of leaf nodes in the Merkle tree. By using these account numbers, we can ensure that the position of the leaf nodes in the Merkle tree is always the same. This approach allows us to avoid rebuilding the Merkle tree whenever an account or validator’s state changes. Instead, we can save the previous Merkle tree and recalculate the parent hashes by fetching neighbor hashes as needed. This helps to ensure scalability and reduces the computational resources required for recalculating the Merkle tree.
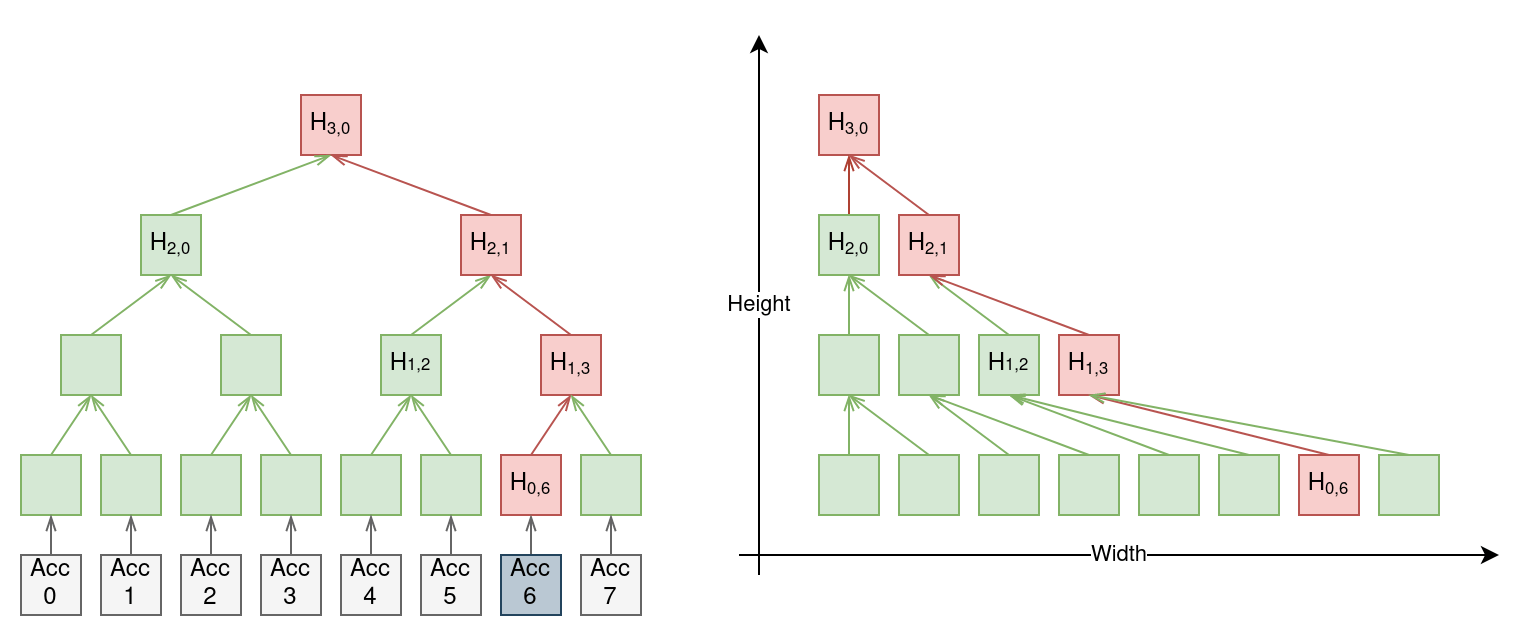
In this example, only account 6 has been updated. By locating the corresponding leaf node in the existing Merkle tree and traversing the tree towards the root node, we can calculate new root hash. This approach has a complexity of $ O(\log n) $, making it efficient for large numbers of accounts.